



Next: 2 Notacja
Up: 3 Protokół anonimowych mikropłatności
Previous: 3 Protokół anonimowych mikropłatności
Spis rzeczy
Operacje matematyczne na wszystkich etapach obliczeń odbywają się nad ciałami
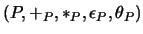 i
i
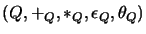 ,
gdzie
,
gdzie 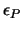 i
i 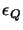 są elementami neutralnymi mnożenia,
a
są elementami neutralnymi mnożenia,
a 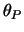 i
i 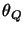 dodawania. Funkcja
dodawania. Funkcja
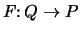 jest
jednokierunkową funkcją, na której opiera się bezpieczeństwo systemu. Funkcja
ta posiada następujące własności:
jest
jednokierunkową funkcją, na której opiera się bezpieczeństwo systemu. Funkcja
ta posiada następujące własności:
Jako 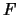 będzie użyta funkcja:
będzie użyta funkcja:
gdzie
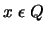 ,
, 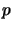 jest liczbą pierwszą,
jest liczbą pierwszą, 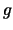 jest generatorem
grupy
jest generatorem
grupy 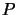 , która jest podgrupą
, która jest podgrupą
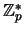 rozmiaru
rozmiaru 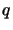 dla
dla 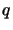 pierwszego,
a
pierwszego,
a
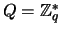 .
.
W protokole wykorzystano jako funkcję bezkolizyjną funkcję haszującą 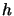 (por. dodatek B). W mojej realizacji protokołu używam funkcji MD5,
na wyniku której (wynik ten traktuję jak liczbę binarną) dokonuję operacji
(por. dodatek B). W mojej realizacji protokołu używam funkcji MD5,
na wyniku której (wynik ten traktuję jak liczbę binarną) dokonuję operacji
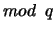 . Wybór funkcji MD5 wynika z faktu, że wynik funkcji haszującej
powinien być tej samej długości co liczba
. Wybór funkcji MD5 wynika z faktu, że wynik funkcji haszującej
powinien być tej samej długości co liczba 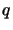 .
.




Next: 2 Notacja
Up: 3 Protokół anonimowych mikropłatności
Previous: 3 Protokół anonimowych mikropłatności
Spis rzeczy
Piotr Kozieradzki
2003-05-16
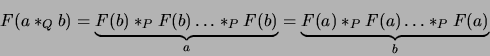
![]() będzie użyta funkcja:
będzie użyta funkcja:
![]() (por. dodatek B). W mojej realizacji protokołu używam funkcji MD5,
na wyniku której (wynik ten traktuję jak liczbę binarną) dokonuję operacji
(por. dodatek B). W mojej realizacji protokołu używam funkcji MD5,
na wyniku której (wynik ten traktuję jak liczbę binarną) dokonuję operacji
![]() . Wybór funkcji MD5 wynika z faktu, że wynik funkcji haszującej
powinien być tej samej długości co liczba
. Wybór funkcji MD5 wynika z faktu, że wynik funkcji haszującej
powinien być tej samej długości co liczba ![]() .
.