



Next: D. Implementacja
Up: C. Obliczenia na niewiarygodnym
Previous: 2 Koszty
Spis rzeczy
Założenia: chcemy ukryć przed serwerem tajny klucz 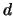 . Nie będziemy
zajmować się ukrywaniem wiadomości
. Nie będziemy
zajmować się ukrywaniem wiadomości 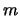 . Bedziemy używać standardowych
oznaczeń:
. Bedziemy używać standardowych
oznaczeń:
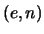 ,
, 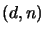 -- klucz jawny i tajny
-- klucz jawny i tajny
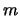 ,
, 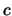 -- wiadomośći kryptogram
-- wiadomośći kryptogram
PROTOKÓŁ:
- Klient losuje wektor liczb całkowitych
![$D = [d_0, d_1,\:\ldots,d_M]$](img241.png) i wektor binarny
i wektor binarny
![$F = [f_0, f_1, \: \ldots, f_M]$](img242.png) , tak że
, tak że
gdzie 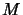 i
i 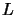 są
pewnymi liczbami naturalnymi.
są
pewnymi liczbami naturalnymi.
- klient wysyła do serwera
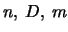 .
serwer oblicza i odsyła do klienta
.
serwer oblicza i odsyła do klienta
![$Z = [z_0, z_1, \ldots, z_M]$](img247.png) , takie że
, takie że
- klient oblicza
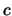 jako
jako 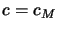 w następujący sposób
w następujący sposób
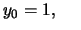
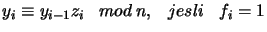
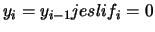
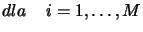
Istnieje tu możliwość określania poziomu bezpieczeństwa przez zmienianie
parametru 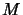 . Łatwo zauważyć, iż nie znając
. Łatwo zauważyć, iż nie znając 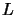 aby znaleźć
aby znaleźć 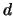 należało by
przeszukać wszystkie
należało by
przeszukać wszystkie 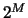 możliwości. Jako że bezpieczeństwo protokołu RSA
jest w szczególności związane wykładniczo z dlugościa kluczy
możliwości. Jako że bezpieczeństwo protokołu RSA
jest w szczególności związane wykładniczo z dlugościa kluczy 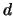 i
i 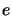 oraz,
że złożoność obliczeniowa opracji postaci
oraz,
że złożoność obliczeniowa opracji postaci
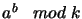 jest rzędu
jest rzędu
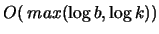 przedstawione powyżej rozwiązanie mozna
bardziej traktować jako inspirację niż pełna i poważną propozycję.
przedstawione powyżej rozwiązanie mozna
bardziej traktować jako inspirację niż pełna i poważną propozycję.




Next: D. Implementacja
Up: C. Obliczenia na niewiarygodnym
Previous: 2 Koszty
Spis rzeczy
Piotr Kozieradzki
2003-05-16
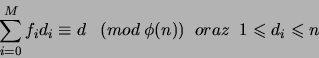
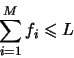
![]() . Łatwo zauważyć, iż nie znając
. Łatwo zauważyć, iż nie znając ![]() aby znaleźć
aby znaleźć ![]() należało by
przeszukać wszystkie
należało by
przeszukać wszystkie ![]() możliwości. Jako że bezpieczeństwo protokołu RSA
jest w szczególności związane wykładniczo z dlugościa kluczy
możliwości. Jako że bezpieczeństwo protokołu RSA
jest w szczególności związane wykładniczo z dlugościa kluczy ![]() i
i ![]() oraz,
że złożoność obliczeniowa opracji postaci
oraz,
że złożoność obliczeniowa opracji postaci
![]() jest rzędu
jest rzędu
![]() przedstawione powyżej rozwiązanie mozna
bardziej traktować jako inspirację niż pełna i poważną propozycję.
przedstawione powyżej rozwiązanie mozna
bardziej traktować jako inspirację niż pełna i poważną propozycję.