



Next: Anonimowe systemy pocztowe ogólnego
Up: Miksy Chauma
Previous: Anonimowy system pocztowy
Spis treści
Opisana w punkcie 2.2.3 technika pozwala na anonimowe wysłanie wiadomości od
użytkownika 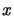 do
do 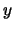 . Pożądana jest teraz możliwość odpowiedzi
. Pożądana jest teraz możliwość odpowiedzi 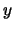 do
do 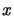 ,
tak aby y nie poznał rzeczywistego adresu
,
tak aby y nie poznał rzeczywistego adresu 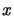 , czyli z zapewnieniem anonimowości
odbiorcy odpowiedzi. Można to zrealizować przez wysłanie do
, czyli z zapewnieniem anonimowości
odbiorcy odpowiedzi. Można to zrealizować przez wysłanie do 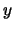 razem
z wiadomością specjalnie przygotowanego ,,adresu zwrotnego'' (przesłanie to
może odbywać się na zasadach opisanych w poprzednim rozdziale).
Adres zwrotny ma postać:
razem
z wiadomością specjalnie przygotowanego ,,adresu zwrotnego'' (przesłanie to
może odbywać się na zasadach opisanych w poprzednim rozdziale).
Adres zwrotny ma postać:
Prawdziwy adres 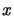 ,
, 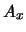 , został tu zapieczętowany kluczem miksu
, został tu zapieczętowany kluczem miksu 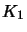 z
użyciem ciągu losowego
z
użyciem ciągu losowego 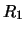 , który posłuży później jako klucz.
, który posłuży później jako klucz.
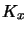 jest kluczem wybranym na potrzeby tego adresu zwrotnego.
Posiadając taką informację
jest kluczem wybranym na potrzeby tego adresu zwrotnego.
Posiadając taką informację 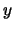 może utworzyć
wiadomość do
może utworzyć
wiadomość do 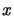 o treści
o treści 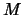 w następujący sposób:
w następujący sposób:
Następnie wysyła tę wiadomość do miksu 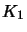 , miks ten wykonuje nową operację:
, miks ten wykonuje nową operację:
Odzyskany z zapieczętowanej wiadomości ciąg losowy 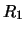 został teraz
wykorzystany do ponownego zaszyfrowania odpowiedzi
został teraz
wykorzystany do ponownego zaszyfrowania odpowiedzi 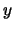 . Nowy miks może teraz
przesłać wiadomość
. Nowy miks może teraz
przesłać wiadomość
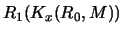 do
do 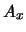 , który jako jedyny może
odczytać treść
, który jako jedyny może
odczytać treść 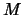 dzięki znajomości
dzięki znajomości 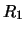 i
i 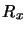 . Klucze
. Klucze 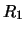 i
i 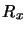 mogą być zarówno kluczami publicznymi jak i symetrycznymi.
mogą być zarówno kluczami publicznymi jak i symetrycznymi.
Podobnie jak w przypadku systemu pocztowego do przesłania wiadomości powrotnej
może zostać użyta kaskada miksów. W tym przypadku ogólna postać adresu
zwrotnego wygląda następująco:
Wiadomość zwrotna przygotowywana jest w sposób analogiczny, jak w przypadku
pojedynczego miksu.
Po przejściu przez pierwszy miks otrzymujemy:
Ostatni miks 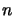 generuje:
generuje:




Next: Anonimowe systemy pocztowe ogólnego
Up: Miksy Chauma
Previous: Anonimowy system pocztowy
Spis treści
Michal Szafranski
2003-11-13
![]() do
do ![]() . Pożądana jest teraz możliwość odpowiedzi
. Pożądana jest teraz możliwość odpowiedzi ![]() do
do ![]() ,
tak aby y nie poznał rzeczywistego adresu
,
tak aby y nie poznał rzeczywistego adresu ![]() , czyli z zapewnieniem anonimowości
odbiorcy odpowiedzi. Można to zrealizować przez wysłanie do
, czyli z zapewnieniem anonimowości
odbiorcy odpowiedzi. Można to zrealizować przez wysłanie do ![]() razem
z wiadomością specjalnie przygotowanego ,,adresu zwrotnego'' (przesłanie to
może odbywać się na zasadach opisanych w poprzednim rozdziale).
Adres zwrotny ma postać:
razem
z wiadomością specjalnie przygotowanego ,,adresu zwrotnego'' (przesłanie to
może odbywać się na zasadach opisanych w poprzednim rozdziale).
Adres zwrotny ma postać: