


Następny: Wyznaczanie priorytetów
Nadrzędny: Algorytm wyznaczania priorytetu
Poprzedni: Zastosowanie sieci neuronowej
Spis rzeczy
Sposób uwzględnienia historii
Drugim z czynników, który wpływa na wartość priorytetu jest zachowanie
komputera mierzone w ciągu ostatnich dwunastu cykli pobierania
danych od modułu wykonawcy. W dalszej części pracy wartość tego składnika
priorytetu będziemy w skrócie nazywać historią.
Oszacowanie historii można przeprowadzać na wiele
sposobów. Najprostszym z nich jest po prostu zsumowanie wartości np. estymatora I ze wszystkich okresów branych pod uwagę. Niestety
otrzymany w ten sposób parametr nie oddaje dobrze zmian w zachowaniu
komputerów. Dlatego uwzględnienie historii zostało oparte na wartości
średniej oraz wariancji estymatora I policzonych dla ostatniej
godziny oraz ostatnich 12 godzin. Przy ustaleniu wielkości kroku na
wartość równą 5 minut przedstawione przedziały odpowiadają 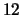 krokom
(ostatnia godzina) i
krokom
(ostatnia godzina) i 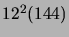 krokom (ostatnie 12 godzin). Na
bazie tych wartości obliczany jest estymator II
krokom (ostatnie 12 godzin). Na
bazie tych wartości obliczany jest estymator II
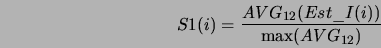 |
(7) |
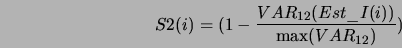 |
(8) |
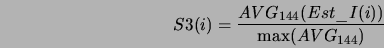 |
(9) |
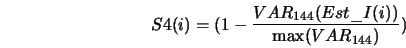 |
(10) |
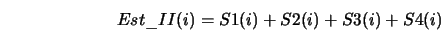 |
(11) |
Oznaczenia:
-
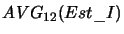 ,
,
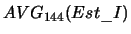 - wartość średnia estymatora I
obliczona odpowiednio na podstawie ostatnich 12 i 144 wartości,
- wartość średnia estymatora I
obliczona odpowiednio na podstawie ostatnich 12 i 144 wartości,
-
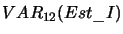 ,
,
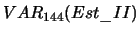 - wartość wariancji
estymatora I z ostatnich 12 i 144 kroków,
- wartość wariancji
estymatora I z ostatnich 12 i 144 kroków,
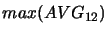 ,
, 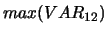 ... -- wartość maksimum
średniej i wariancji z odpowiednio 12 i 144 ostatnich kroków
obliczona dla wszystkich maszyn, których ruch jest analizowany,
... -- wartość maksimum
średniej i wariancji z odpowiednio 12 i 144 ostatnich kroków
obliczona dla wszystkich maszyn, których ruch jest analizowany,
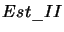 - estymator II.
- estymator II.
Wzór 3.10 wymaga dwóch komentarzy:
- 12 lub 144 ostatnie wartości brane do obliczania średniej
i wariancji estymatora I uwzględniają wartość szacowaną dla
następnego kroku. Zgodnie z tym co napisano w p. 3.2.2
jest to liczba otrzymana na wyjściu sieci neuronowej. Dzięki
temu zabiegowi podobnie jak dla estymatora I, wielkość
estymatora II uwzględnia na bieżąco zmiany w obciążeniu
bramy.
- Z postaci zależności 3.10 wynika, że wielkość
estymatora II jest tym większa im większa jest średnia
estymatora I i tym większa im mniejsza jest jego
wariancja. Wynika to głównie z następującego heurystycznego
podziału komputerów na cztery grupy ze względu na
charakterystykę ruchu, który generują.
- Grupa 1 - duża średnia i mała wariancja - obejmuje
maszyny, które przez długi okres transmitują dużo danych (duża
wartość estymatora I) i na praktycznie stałym poziomie (mała
wartość wariancji).
- Grupa 2 - duża średnia i duża wariancja - należą do niej
komputery, które miewają duże transfery danych (duża średnia),
jednak nie trwają one ciągle, tylko mają formę krótkotrwałych
okresów wysokiej aktywności (duża wariancja).
- Grupa 3 - mała średnia i duża wariancja - to głównie
maszyny, które przesyłają mało danych (mała średnia) i robią to
sporadycznie (duża wariancja).
- Grupa 4 - mała średnia i mała wariancja - obejmuje te
komputery, które systematycznie (mała wariancja) wykorzystują
niewielki kawałek pasma (mała średnia).
Najbardziej niepożądane w sytuacji obciążenia pasma jest zachowanie
charakterystyczne dla grupy 1 opisywanej przez dużą średnią i małą wariancję.
Odwrócenie we wzorze na estymator II zależności od wariancji sprawia, że jego
wartość jest odwrotnie proporcjonalna do numeru grupy i dzięki temu
rozdzielenie komputerów pomiędzy grupy jest możliwe na podstawie jego
wielkości.
Estymator II jest obliczany na podstawie estymatora I jednak również w tym
spełniona jest reguła: wartość priorytetu jest odwrotnie proporcjonalna do
wielkości estymatora II.
Estymator I oraz estymator II stanowią dwa dobrze zdefiniowane parametry, na
podstawie których można rozdzielić wszystkie analizowane
komputery na podzbiory. Każdy z takich podzbiorów - klasa komputerów -
jest charakteryzowany przez wartość priorytetu.



Następny: Wyznaczanie priorytetów
Nadrzędny: Algorytm wyznaczania priorytetu
Poprzedni: Zastosowanie sieci neuronowej
Spis rzeczy
Marcin Kaszyński, Krzysztof Lorek
![]() krokom
(ostatnia godzina) i
krokom
(ostatnia godzina) i ![]() krokom (ostatnie 12 godzin). Na
bazie tych wartości obliczany jest estymator II
krokom (ostatnie 12 godzin). Na
bazie tych wartości obliczany jest estymator II