



Next: 3 Generator liczb losowych,
Up: 5 Projekt
Previous: 1 Operacje mnożenia i
Spis rzeczy
2 Tworzenie kluczy
Są dwa aspekty tworzenia kluczy używanych w protokołach podpisów Schnorra
i protokole częściowo ślepych podpisów. Na początku należy wybrać parametry
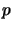 i
i 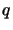 , które są dużymi liczbami pierwszymi. Liczby te należy dobrać tak,
by łatwo można było obliczyć generator
, które są dużymi liczbami pierwszymi. Liczby te należy dobrać tak,
by łatwo można było obliczyć generator 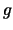 podgrupy
podgrupy
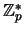 rozmiaru
rozmiaru
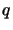 . Aby móc go wyznaczyć stosunkowo szybko, należy pamiętać, że
. Aby móc go wyznaczyć stosunkowo szybko, należy pamiętać, że
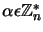 jest generatorem grupy
jest generatorem grupy
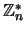 wtedy i tylko wtedy gdy:
wtedy i tylko wtedy gdy:
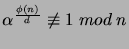 dla
dla 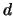 będących dzielnikami
będących dzielnikami 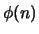
dla liczby pierwszej 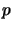
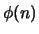 równa się oczywiście
równa się oczywiście 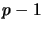 . Zatem użyto
następującego algorytmu:
. Zatem użyto
następującego algorytmu:
start:
znajdź liczbę pierwszą B
for i := 1 to 1000 do
znajdź liczbę pierwszą A
policz P := A * B * 2 + 1;
jeżeli P jest liczba pierwszą, to return (A, B, P)
end for;
idź do "start"
Ten algorytm daje nie tylko liczbę pierwszą 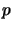 , ale też rozkład
, ale też rozkład
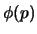 . Warto zaznaczyć, że
. Warto zaznaczyć, że 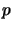 jest bezpieczną liczbą pierwszą, czyli taką,
dla której
jest bezpieczną liczbą pierwszą, czyli taką,
dla której 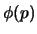 ma duży dzielnik pierwszy. Dobierając
odpowiednie parametry można spowodować, by
ma duży dzielnik pierwszy. Dobierając
odpowiednie parametry można spowodować, by 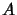 było takiej długości, aby dało się
go używać w protokole jako
było takiej długości, aby dało się
go używać w protokole jako 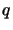 . Ważne jest, by jako pierwsze losować
. Ważne jest, by jako pierwsze losować 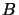 ,
którego długość powinna wynosić
,
którego długość powinna wynosić 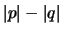 (w implementowanym protokole
(w implementowanym protokole
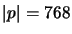 , a
, a 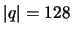 ). Wynika to z faktu, iż im dłuższa jest liczba
pierwsza, tym dłużej trwa jej znalezienie. Ta część obliczeń jest bardzo
czasochłonna, ale jest wykonywana tylko raz i to przez serwery instytucji
certyfikującej, gdyż wszyscy uczestnicy protokołu będą posługiwali się tymi
samymi parametrami.
). Wynika to z faktu, iż im dłuższa jest liczba
pierwsza, tym dłużej trwa jej znalezienie. Ta część obliczeń jest bardzo
czasochłonna, ale jest wykonywana tylko raz i to przez serwery instytucji
certyfikującej, gdyż wszyscy uczestnicy protokołu będą posługiwali się tymi
samymi parametrami.
Na komputerze z procesorem Celeron 300A taka operacja dla 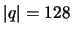 i
i 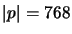 zajmowała od 55 sekund do 8 minut.
zajmowała od 55 sekund do 8 minut.
By znaleźć generator grupy
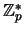 użyto następującej procedury
(A, B, P to wartości policzone poprzednio):
użyto następującej procedury
(A, B, P to wartości policzone poprzednio):
start:
znajdź liczbę pierwszą H mniejszą od P
jezeli ( H^A modulo P == 1) idz do "start"
jezeli ( H^B modulo P == 1) idz do "start"
jezeli ( H^2 modulo P == 1) idz do "start"
return H
Pozwala ona na obliczenie generatora grupy
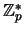 , jednak w protokole
używane jest
, jednak w protokole
używane jest 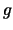 , które jest generatorem podgrupy
, które jest generatorem podgrupy
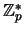 rozmiaru
rozmiaru
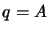 . Poszukiwane
. Poszukiwane 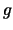 oblicza się używając wzoru:
oblicza się używając wzoru:
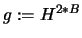
Kolejnym etapem jest utworzenie kluczy prywatnych i publicznych dla użytkowników
systemu. Obliczenia te sprowadzają się tylko do wylosowania elementu
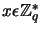 , który będzie kluczem prywatnym i policzenia klucza
publicznego
, który będzie kluczem prywatnym i policzenia klucza
publicznego
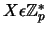 jako
jako
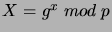 .
.




Next: 3 Generator liczb losowych,
Up: 5 Projekt
Previous: 1 Operacje mnożenia i
Spis rzeczy
Piotr Kozieradzki
2003-05-16
dla
będących dzielnikami
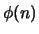
![]() użyto następującej procedury
(A, B, P to wartości policzone poprzednio):
użyto następującej procedury
(A, B, P to wartości policzone poprzednio):
![]() , który będzie kluczem prywatnym i policzenia klucza
publicznego
, który będzie kluczem prywatnym i policzenia klucza
publicznego
![]() jako
jako
![]() .
.