Drugą operacją mającą znaczący wpływ na czas generacji kluczy i tworzenia podpisów
jest operacja potęgowania w grupie
![]() . Jest ona wykorzystywana również
w algorytmie generacji liczb pierwszych w teście Millera-Rabina [3].
Należy zauważyć, iż w czasie generacji poświadczeń elektronicznych wykonuje
się operacje
. Jest ona wykorzystywana również
w algorytmie generacji liczb pierwszych w teście Millera-Rabina [3].
Należy zauważyć, iż w czasie generacji poświadczeń elektronicznych wykonuje
się operacje
![]() , gdzie
, gdzie ![]() i
i ![]() są stałymi. Zatem,
by policzyć
są stałymi. Zatem,
by policzyć ![]() wystarczy mieć
wystarczy mieć ![]() i
i ![]() , takie że
, takie że ![]() oraz policzone uprzednio
oraz policzone uprzednio
![]() i
i
![]() . Wtedy łatwo możemy obliczyć
. Wtedy łatwo możemy obliczyć
![]() . Niestety zapamiętywanie wszystkich obliczanych
potęg jest bardzo kosztowne i niezgodne z prawem (por dodatek A).
Pewnym rozwiązaniem jest zapamiętanie wszystkich potęg postaci
. Niestety zapamiętywanie wszystkich obliczanych
potęg jest bardzo kosztowne i niezgodne z prawem (por dodatek A).
Pewnym rozwiązaniem jest zapamiętanie wszystkich potęg postaci ![]() dla
dla
![]() . Można wtedy użyć następującego
algorytmu:
. Można wtedy użyć następującego
algorytmu:
i:=1
for d := 0 to length( g )
if x[d] = 1 then i := i * a[d] mod p;
return i;
W tablicy ![]() przechowujemy zapamiętane
przechowujemy zapamiętane ![]() .
.
Można oczywiście przechowywać obliczone wartości postaci
![]() ,
gdzie
,
gdzie ![]() to niewielkie liczby z przedziału
to niewielkie liczby z przedziału ![]() . Wtedy:
. Wtedy:
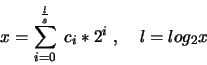
Niech ![]() , a
, a
![]() . Wtedy algorytm
będzie wyglądał następująco:
. Wtedy algorytm
będzie wyglądał następująco:
y := x;
i:=1;
for d := 0 to l
i := i * a[d][y mod r] mod p;
y := y div r;
return i;
Jednak w tym przypadku skorzystano z tradycyjnego algorytmu
,,podnoś do kwadratu i mnóż''.
Korzystamy wtedy z reprezentacji liczby ![]() :
:
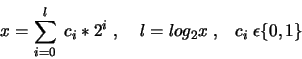
i := x[l];
for d := (l - 1) downto 0
i := i * i mod p;
if x[d] = 1 then i := i * a mod p;
return i;
W czasie implementacji brano pod uwagę wykorzystanie funkcji realizującej
taką operację, wchodzącej w skład biblioteki bignat. Niestety kod tej
funkcji zawiera pętlę for, której implementacja w języku funkcyjnym jest
bardzo niewydajna. Zapis funkcji umożliwiający wykorzystanie przez kompilator
optymalizacji rekursji ogonowej przyspieszył czas wykonywania potęgowania ponad
27 krotnie. W tabeli 5.1 przedstawiono czasy poszczególnych operacji
dla ![]() ,
, ![]() i
i ![]() równych 1024. Użyto takich długości, by test był
porównywalny z najczęściej spotykanymi wynikami dotyczącymi algorytmu RSA.
równych 1024. Użyto takich długości, by test był
porównywalny z najczęściej spotykanymi wynikami dotyczącymi algorytmu RSA.