- Liczba cyfr liczby naturalnej:
val num_digits_natE : Nat.nat -> int
- Przekazuje nową liczbę mniejszą o jeden od argumentu:
val decr_natE : Nat.nat -> Nat.nat
- Przekazuje nową liczbę większą o jeden od argumentu:
val incr_natE : Nat.nat -> Nat.nat
- Suma argumentów:
val add_natE : Nat.nat -> Nat.nat -> Nat.nat
- Różnica argumentów:
val sub_natE : Nat.nat -> Nat.nat -> Nat.nat
- iloczyn argumentów:
val mult_natE : Nat.nat -> Nat.nat -> Nat.nat
- Kwadrat argumentu:
val square_natE : Nat.nat -> Nat.nat
- Wartość pierwszego argumentu modulo drugi argument:
val mod_natE : Nat.nat -> Nat.nat -> Nat.nat
- Iloraz pierwszego argumentu przez drugi:
val div_natE : Nat.nat -> Nat.nat -> Nat.nat
- Iloraz pierwszego argumentu przez drugi wynikiem jest para: pierwszy
element to wynik dzielenia argumentów, a drugi to reszta z tego dzielenia:
val div_mod_nat_natE : Nat.nat -> Nat.nat -> Nat.nat * Nat.nat
- Wylosowana liczba z przedziału
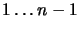 , gdzie
, gdzie 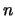 to
pierwszy argument:
to
pierwszy argument:
val losuj_przedzial : Nat.nat -> Nat.nat
- Poniższa funkcja została napisana przeze mnie gdyż opierając się na
implementacji funkcji z biblioteki bignat, która jest rozszerzeniem
biblioteki nat nie mogłem uzyskać zadowalającej wydajności. Dopiero
implementacja rekurencyjna dająca możliwość wykorzystania optymalizacji
rekursji ogonowej przyspieszyła tę funkcję ponad 26 razy.
val power_nat_nat_mod : Nat.nat -> Nat.nat -> Nat.nat -> Nat.nat
- Poniższe funkcje, opisane dokładniej w rozdziale 5.3 służą do
sprawdzenia, czy dana liczba jest liczbą pierwszą
val witness_nat : Nat.nat -> Nat.nat -> bool
val miller_rabin_nat : Nat.nat -> int -> bool
val pseudo_prime_exp : Nat.nat -> bool
val test_pseudoprime : Nat.nat -> bool
- Ta funkcja przekazuje liczbę pierwszą z przedziału
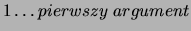 . Pierwszość
. Pierwszość 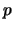 sprawdzam na dwa sposoby;
najpierw jest test
sprawdzam na dwa sposoby;
najpierw jest test
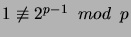 . A następnie,
jeżeli odpowiedź była pozytywna, wykonuję test Millera-Rabina.
. A następnie,
jeżeli odpowiedź była pozytywna, wykonuję test Millera-Rabina.
val l_pierwsza_przedzial_nat : Nat.nat -> Nat.nat
- Funkcja przekazuje największy wspólny dzielnik dwóch liczb będących jej
argumentami. Wykorzystuje klasyczny algorytm Euklidesa opisany
w książce ,,Wprowadzenie do algorytmów'' [3].
val gcd_nat : Nat.nat -> Nat.nat -> Nat.nat
- Rozszerzona wersja wspomnianego powyżej algorytmu. W piątce
uporządkowanej będącej wynikiem (nazwijmy ją
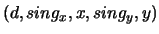 )
)
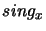 i
i 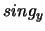 , których dopuszczalne wartości to
, których dopuszczalne wartości to 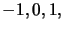 interpretowane są jako znaki liczb odpowiednio
interpretowane są jako znaki liczb odpowiednio 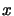 i
i 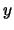 . Wywołanie
eX_gcd_nat_f a b da
. Wywołanie
eX_gcd_nat_f a b da
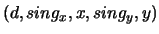 , takie że
, takie że
val eX_gcd_nat_f :
Nat.nat -> Nat.nat -> Nat.nat * int * Nat.nat * int * Nat.nat
- Ta funkcja jest tylko pomocniczą funkcja testową, która dokonuje
przedstawionego powyżej obliczenia.
val suma_iloczynow :
Nat.nat -> int -> Nat.nat -> Nat.nat -> int -> Nat.nat -> Nat.nat -> unit
- Daje liczbę wybrana losowo liczbę z przedziału
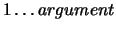 ,
która jest względnie pierwsza z
,
która jest względnie pierwsza z 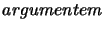 :
:
val give_prime_with : Nat.nat -> Nat.nat
- Jako wynik otrzymujemy
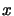 , takie że:
, takie że:
val reverce_mod : Nat.nat -> Nat.nat -> Nat.nat
- Ta funkcja znajduje bezpieczną liczbę pierwszą mniejszą od pierwszego
argumentu. Bezpieczna liczba pierwsza
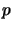 to taka liczba, że
to taka liczba, że 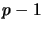 posiada
duży dzielnik pierwszy. Wprowadziłem tu następujący algorytm:
posiada
duży dzielnik pierwszy. Wprowadziłem tu następujący algorytm:
start:
znajdź liczbę pierwszą q mniejszą od połowy pierwszego argumentu
p := 2 * q + 1;
jeżeli p jest liczbą pierwszą to return p
wpp. idź do start
Wynikiem działania funkcji jest wyliczona wartość 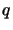 i
i 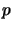 .
.
val find_safe_prime_2_less : Nat.nat -> Nat.nat * Nat.nat
- Ta funkcja jest podobna do pierwszej z tym, że poszukiwana jest liczba
pierwsza postaci
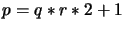 . Liczbę pierwszą
. Liczbę pierwszą 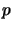 obliczam
w następujący sposób:
obliczam
w następujący sposób:
start:
znajdź liczby pierwsze q i r
p := 2 * q * r + 1;
jeżeli p jest liczbą pierwszą, to return p
wpp. idź do start
Potrzeba istnienia takiej funkcji została szczegółowo wyjaśniona w rozdziale
5.2:
val find_safe_prime_3_less :
Nat.nat -> Nat.nat -> Nat.nat * Nat.nat * Nat.nat
- Funkcja ta przekazuje parę liczb
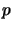 i
i 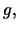 takich że
takich że 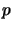 jest
bezpieczną liczbą pierwszą mniejszą od argumentu funkcji, a
jest
bezpieczną liczbą pierwszą mniejszą od argumentu funkcji, a 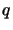 jest
generatorem
jest
generatorem
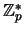 .
.
val generator_grupy : Nat.nat -> Nat.nat * Nat.nat
- Funkcja wypisuje w postaci zero-jedynkowej liczbę typu nat:
val write_nat_bi : Nat.nat -> unit
- Funkcja konwertuje liczbę typu nat do napisu typu string:
val make_oct_from_nat : Nat.nat -> string
- Funkcja konwertuje napis typu string do liczby typu nat:
val make_nat_from_oct : string -> Nat.nat
- Funkcja oblicza wartość funkcji MD5 na argumencie:
val hash_MD5_nat : Nat.nat -> Nat.nat
- Funkcja oblicza wartość funcji MD5 na napisie złożonym z dwóch pierwszych
argumentów poddanych konwersji do typu string; w wyniku otrzymujemy
wartość typu nat:
val hash_MD5_nat_nat : Nat.nat -> Nat.nat -> Nat.nat
- Funkcja najpierw dokonuje konwersji pierwszego argumentu do napisu
później konkatenuje go z drugim argumentem i oblicza na nim wartość funkcji
MD5, którą przekazuje jako liczbę typu nat:
val hash_MD5_nat_string : Nat.nat -> string -> Nat.nat