Przedstawiony poniżej protokół, mimo iż jest bardzo podobny do protokołu ślepych
podpisów Schnorra pozwala podzielić podpisywaną przez ![]() wiadomość na dwie
części: tajną
wiadomość na dwie
części: tajną ![]() i jawną
i jawną ![]() . Dzięki temu strona żądająca podpisu może ukryć
tą część wiadomości, która pozwoliłaby rozpoznać ją w przyszłości. Z kolei
. Dzięki temu strona żądająca podpisu może ukryć
tą część wiadomości, która pozwoliłaby rozpoznać ją w przyszłości. Z kolei
![]() uzyskuje możliwość weryfikacji kluczowych danych. Przebieg protokołu
gwarantuje, iż obie części --
uzyskuje możliwość weryfikacji kluczowych danych. Przebieg protokołu
gwarantuje, iż obie części -- ![]() i
i ![]() zostają sklejone i nie można żadnej
z nich podmienić.
zostają sklejone i nie można żadnej
z nich podmienić.
Protokół częściowo ślepych podpisów bazuje na protokole podpisów cyfrowych
Nymerga-Ruppela, a także modyfikacji dotyczącej używanych kluczy, podanej
w [5]. Protokół pod względem budowy jest podobny do protokołu ślepych
podpisów Schnorra. Jego ideą jest zawarcie ![]() -- ujawnionej części wiadomości
-- w kluczu prywatnym i publicznym transakcji, generowanym przez stronę
podpisującą S. W tym celu używa się dwóch publicznych wielomianów:
-- ujawnionej części wiadomości
-- w kluczu prywatnym i publicznym transakcji, generowanym przez stronę
podpisującą S. W tym celu używa się dwóch publicznych wielomianów:
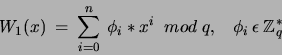
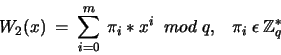
liczy
liczy
losujei wysyła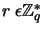
liczy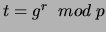
V może teraz zweryfikować podpis w następujący sposób: