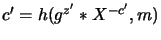2 Ślepe podpisy Schnorra

Warto sobie uświadomić czym grożą jawne podpisy. Wyobraźmy sobie system związany z elektroniczna gotówką, w którym użytkownicy pragną zachować anonimowość. Strona wydająca poświadczenia elektroniczne, współpracując ze sklepami (np. bank odbiera podpisane monety), mogłaby ustalić i przypisać do klienta wszystkie jego transakcje. Istnieje jednak niebezpieczeństwo, że strona podpisująca poświadczy nieprawdę. Można się przed tym bronić na różne sposoby.

Jedną z metod jest protokół mogący służyć wydawaniu identyfikatorów. Strona chcąca uzyskać identyfikator przygotowuje wiele np. 1000 dopuszczalnych identyfikatorów. Bank podpisuje je na ślepo, a następnie żąda wydania mu 999 wylosowanych przez siebie certyfikatów. Jeżeli okażą się one poprawne, to uznaje, że ten ostatni też jest dobry. Prawdopodobieństwo oszustwa wynosi $\frac{1}{1000}$ i można je skalować.

Inną metodą, którą można zastosować w implementowanym tu protokole, jest metoda anonimowych mikropłatności. Zgodnie z nią należy przygotować zestaw par (klucze, typ wiadomości). W protokole dla banku ważna jest tylko wartość banknotu. Pozostałych informacji, takich jak klucze publiczne transakcji i klienta, bank nie musi poznać. Gdyby ograniczyć dopuszczalne nominały, wtedy posługując się różnymi kluczami dla różnych nominałów moglibyśmy zagwarantować to, że klient nie oszuka banku zwiększając wartość monety elektronicznej. Rozwiązanie to ma jednak dwie poważne wady. Używa się tu dużej liczby kluczy, które przecież każda ze stron musi przechowywać. Drugim, być może poważniejszym ograniczeniem, jest to, że banknot nie może mieć dowolnej wartości. Trzeba przypomnieć sobie również o dacie, która miała określać termin ważności banknotu. Nawet gdyby była ona określana z dokładnością do dnia, to i tak w trakcie istnienia systemu każda ze stron musiałaby codziennie zwiększać listę kluczy publicznych.

Protokół ślepych podpisów Schnorra jest dobrym wprowadzeniem do protokołu częściowo ślepych podpisów. W jego opisie zastosowano notacji z rozdziału 4.1. Celem protokołu jest wygenerowanie przez użytkownika trójki liczb $(m,\: c\lq ,\:z\lq )$, która jest (statystycznie) niezależna od trójki $(m,\:c,\:z)$ dostarczonej przez osobę podpisującą.

Protokół ślepych podpisów Schnorra obejmuje następujące kroki:

• R losuje dwie wartości $\alpha$ i $\beta$ należące do $Z_q$;
• S losuje $r$ i oblicza $k \; = \; g^r$;
• użytkownik oblicza odpowiedź $c = H(g^{r + \alpha} \: k^\beta, \;m) + \beta \;\; mod \;q$ i odsyła ją stronie podpisującej;
• S oblicz $z = r + x * c \;\; mod\;q$ i wysyła ją do R;
• R oblicza $c\lq = c - \beta \;\; mod\; q$ i $z\lq = z - \alpha \;\; mod\;q$;

Para $(c', \:z')$ jest podpisem pod $m$.

V może teraz zweryfikować podpis w następujący sposób:

$c' = h(g^{z'} * X^{-c'}, m)$

Wynika to z następujących przekształceń:

$g^{z'} * X^{-c'} =$
$\;\;\; = g^{ r + c * x + \alpha } * X^{-x*c + x*\beta} =$
$\;\;\; = g^{ r + c * x + \alpha } * g^{-x*c} * X^{\beta} =$
$\;\;\; = g^{r + \alpha} * g^{c*x} * g^{-c*x} * X^{\beta} =$
$\;\;\; = g^{r + \alpha} * X^{\beta}$