Przypadek jest nieodłącznym elementem naszego codziennego życia. Wiele zdarzeń, które dzieją się wokół nas, interpretujemy jako przypadkowe. Z tego właśnie powodu ludzkość dąży do ujarzmienia losowości, w czym swój udział ma również - czy może raczej: przede wszystkim - matematyka.
Dziedziną matematyki, która zajmuje się losowością, jest rachunek prawdopodobieństwa. Historycznie dziedzina ta była powszechnie uznawana za coś w rodzaju substytutu wiedzy. Określenie to jest przynajmniej do pewnego stopnia trafne, zaś aby je zobrazować, przywołajmy klasyczny z dydaktycznego punktu widzenia przykład rzutu symetryczną, sześcienną kostką do gry. Znając wszystkie parametry początkowe (takie jak położenie w przestrzeni, prędkość, szybkość rotacji itp.) kostki gdy opuszcza ona naszą dłoń w czasie rzutu oraz znając dodatkowo warunki zewnętrzne towarzyszące rzutowi, takie jak choćby prędkość wiatru, bylibyśmy w stanie obliczyć, ile oczek wypadnie na kostce. Być może teraz uśmiechasz się, drogi czytelniku, na samą myśl o tym, że ktokolwiek rzucający kostką mierzy i określa wszystkie wspomniane powyżej wielkości. Rzecz jasna nikt tego nie robi - bez wątpienia prościej i wygodniej jest potraktować wynik rzutu kostką jako coś losowego, bez względu na to, czy mamy istotnie do czynienia ze zjawiskiem fundamentalnie losowym, czy też zjawiskiem deterministycznym, lecz zbyt skomplikowanym, aby wyznaczyć wynik końcowy.
Ostatnie zdanie wskazuje raczej na problem natury filozoficznej, a problemy filozoficzne najlepiej zostawić filozofom. Matematyk-teoretyk nie potrzebuje znać odpowiedzi na pytanie o istnienie losowości bądź determinizmu w świecie, aby zajmować się rachunkiem prawdopodobieństwa. Może on zwyczajnie założyć, że abstrakcyjne obiekty, które bada, charakteryzują się czymś w rodzaju fundamentalnej losowości, bez względu na możliwość rzeczywistego spełnienia przyjętych założeń i postawionych postulatów. Dbałość o ich spełnienie przynależy raczej do statystyki.
W pierwszej kolejności należy zdać sobie sprawę z tego, że na świecie istnieją w pewnym sensie różne rodzaje losowości. Wróćmy na moment do przykładu z rzutem kostką - liczbę oczek, która wypadnie, możemy potraktować jako losowanie liczby ze zbioru \(\{1, 2, 3, 4, 5, 6\}\) w sytuacji, gdy wszystkie możliwości są równoprawdopodobne. Moglibyśmy teraz wyobrazić sobie inną kostkę, źle wyważoną, na której dwa oczka wypadają o wiele rzadziej, zaś jedno o wiele częściej niż na kostce dobrze wyważonej. Rzut taką kostką również potraktujemy jak losowanie ze zbioru \(\{1, 2, 3, 4, 5, 6\}\), lecz w tym przypadku poszczególne liczby nie są równoprawdopodobne. Niech \(X\) oznacza liczbę oczek, która wypadła na kostce. Możemy przykładowo zadać: $$\mathbb{P}(X=1)=\frac{1}{12},\ \mathbb{P}(X=2)=\frac{1}{12},\ \mathbb{P}(X=3)=\frac{1}{3},\ \mathbb{P}(X=4)=\frac{1}{6},\ \mathbb{P}(X=5)=\frac{1}{6},\ \mathbb{P}(X=6)=\frac{1}{6}$$ Dla porządku wyjaśnimy, że napis \(\mathbb{P}(X=1)=\frac{1}{12}\) należy czytać: prawdopodobieństwo, że na kostce wyrzucimy jedno oczko, wynosi \(\frac{1}{12}\).
Matematyk powie w takiej sytuacji, że zadał rozkład prawdopodobieństwa zmiennej losowej \(X\). Rozkład, nieformalnie mówiąc, to komplet informacji o danym zjawisku losowym. W tym przypadku podaliśmy prawdopodobieństwa wszystkich zdarzeń, które potencjalnie mogą zajść, więc w świetle powyższej "definicji" zadaliśmy rozkład prawdopodobieństwa. Zwróćmy uwagę na fakt, że zadane prawdopodobieństwa muszą dać w sumie \(1\).
Jeśli mamy do czynienia ze skończoną liczbą potencjalnych zdarzeń, sytuacja nie jest skomplikowana i na większość postawionych wówczas pytań potrafimy względnie łatwo odpowiadać. Ciekawiej robi się w momencie, gdy możliwych zdarzeń mamy nieskończenie wiele. Możemy na przykład wyobrazić sobie zakład ubezpieczeniowy, do którego każdego dnia spływają od klientów zgłoszenia szkód. Możliwa liczba szkód zgłoszonych danego dnia będzie bez wątpienia liczbą naturalną, tzn. liczbą ze zbioru \(\{0, 1, 2, ...\}\). Ubezpieczyciel nie wie, ile szkód zostanie zgłoszonych danego dnia, więc stosuje substytut wiedzy - rachunek prawdopodobieństwa. Do matematycznego opisu takiego modelu może posłużyć tzw. rozkład Poissona. Gdy oznaczymy dzienną liczbę zgłoszeń o szkodach przez \(N\), to możemy zadać: $$\mathbb{P}(N=k)=\frac{\lambda^k}{k!}e^{-\lambda}$$
Ryc. 1. Wzór na prawdopodobieństwa w rozkładzie Poissona. Znając wartość parametru \(\lambda\) jesteśmy w stanie przy użyciu tego wzoru obliczyć prawdopodobieństwo dowolnego zdarzenia - wystarczy podstawić interesującą nas wartość \(k\).
gdzie \(\lambda>0\) jest pewną z góry ustaloną liczbą, zaś \(k\) może być dowolną liczbą naturalną. Mamy tu do czynienia z nieskończoną liczbą możliwych zdarzeń. Zauważmy, że gdy znamy wartość \(\lambda\), to znamy także wartość prawdopodobieństwa, że danego dnia spłynie nam zadana liczba zgłoszeń o szkodach. Mamy zatem komplet informacji o zmiennej losowej - zadaliśmy rozkład.
Z jeszcze inną sytuacją będziemy mieli do czynienia, gdy przejdziemy do modelowania zdarzeń typu ciągłego. Wyobraźmy sobie, że potraktujemy średni procentowy wynik z matury rozszerzonej z matematyki w Polsce jako zmienną losową. Po chwili namysłu dojdziemy do wniosku, że tak określona zmienna losowa będzie miała rozkład zupełnie innego typu niż te, które omawialiśmy dotychczas. Rozsądnie jest przyjąć tu model, w którym zmienna przyjmuje dowolną wartość z odcinka \([0, 1]\), a w takiej sytuacji z pewnych istotnych powodów nie możemy zadać rozkładu używając napisów typu \(\mathbb{P}(X=x)=p\). Trudność wynika tu z tego, że nieskończoność liczb w odcinku \([0, 1]\) jest inną, "większą" nieskończonością niż ta związana z liczbami naturalnymi.
Uważny czytelnik zapewne spostrzegł, że przy okazji omawiania rozkładu Poissona nie poruszyliśmy kwestii tego, czy prawdopodobieństwa wszystkich potencjalnych zdarzeń sumują się do \(1\). Rzeczywiście: $$\sum_{k=0}^{+\infty}{\mathbb{P}(N=k)}= \sum_{k=0}^{+\infty}{\frac{\lambda^k}{k!}e^{-\lambda}}= e^{-\lambda}\sum_{k=0}^{+\infty}{\frac{\lambda^k}{k!}}= e^{-\lambda}e^{\lambda}=1$$ W przypadku liczb naturalnych, choć jest ich nieskończenie wiele, daje się stworzyć listę ich wszystkich. Możemy zacząć wypisywać liczby naturalne: \(0, 1, 2, ...\), a zatem możemy także używać napisu \(\sum_{k=0}^{+\infty}\), który znaczy: "rozpoczynając od \(k=0\) dodawaj...". Taki napis jest możliwy wyłącznie dzięki temu, że nieskończoność związana z liczbami naturalnymi jest... w pewnym sensie mała.
Nieskończoność, którą można "wypisać na liście", nazwiemy przeliczalną. Intuicyjnie, przeliczalna nieskończoność to taka, jak ta związana z liczbami naturalnymi. Dodając do siebie przeliczalnie wiele liczb dodatnich możemy uzyskać skończoną wartość - za przykład niech posłuży dobrze znany z liceum szereg geometryczny \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...=1\).
Nieskończoność taka jak ta związana z liczbami rzeczywistymi, np. ilość liczb w odcinku \((0, 1)\) nie jest przeliczalna - jest to "większa" nieskończoność niż ta związana z liczbami naturalnymi. Nieskończoności tego typu nie można "wypisać na liście". Podobnie nieprzeliczalna suma liczb dodatnich w wyniku zawsze da nieskończoność.
Nie istnieje natomiast coś takiego jak lista wszystkich liczb z odcinka \([0, 1]\), a w konsekwencji nie ma sensu napis \(\sum_{x\in[0, 1]}\). Ponadto, gdyby prawdopodobieństwo wylosowania konkretnej wartości było liczbą dodatnią, wszystkie prawdopodobieństwa nie dodałyby się do \(1\), a jest to cecha bezwzględnie wymagana. Należy więc przyjąć model, w którym prawdopodobieństwo wylosowania konkretnej wartości jest równe \(0\).
Można o tym myśleć następująco - nieprzeliczalna nieskończoność jest tak duża, że dodając do siebie nieprzeliczalnie wiele zer dostaniemy w wyniku coś dodatniego!
Pozostawiając tę krótką dygresję o nieskończonościach, zadanie rozkładu prawdopodobieństwa nie polega w takiej sytuacji na wypisaniu kompletnej listy prawdopodobieństw przyjęcia każdej możliwej wartości. W zamian zadajemy funkcję, którą nazywamy gęstością rozkładu prawdopodobieństwa. Jest to funkcja o wartościach nieujemnych, której dziedziną jest \(\mathbb{R}\). Dzięki niej daje się określać prawdopodobieństwa tego, że zmienna losowa przyjmuje wartości wpadające w pewien przedział. Rozkładem ciągłym nazwiemy taki rozkład, który ma gęstość. Rozkład, który nie jest ciągły, nazwiemy dyskretnym. Dla rozkładów dyskretnych, takich jak przy okazji rzutu kostką lub zakładu ubezpieczeniowego (rozkład Poissona), wprowadzanie funkcji gęstości rozkładu nie jest konieczne.
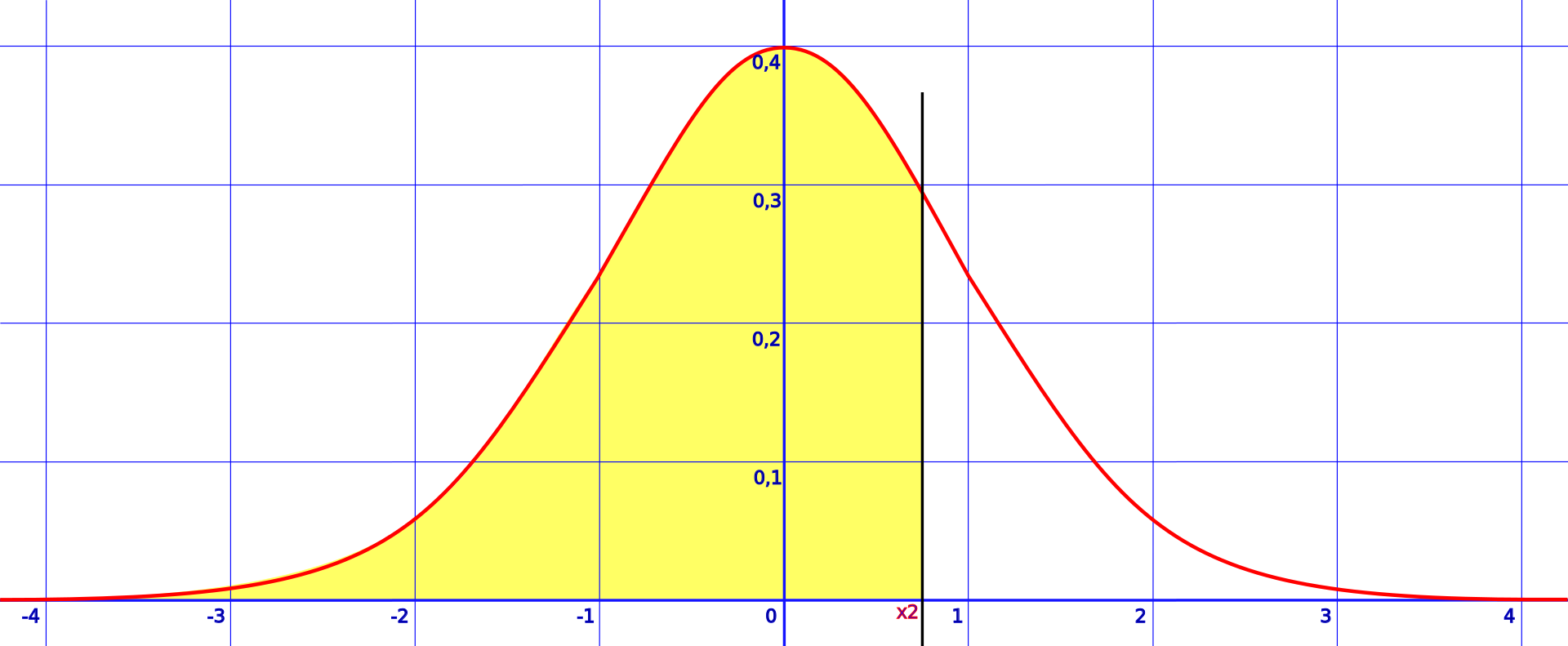
Ryc. 2. Wykres przykładowej funkcji gęstości rozkładu prawdopodobieństwa.
Wyjaśnijmy, co przedstawia wykres na Ryc. 2. - czerwona linia to wykres funkcji gęstości rozkładu prawdopodobieństwa. Wartości, które może przyjmować zmienna losowa, są zaznaczone na osi \(OX\). Wartości funkcji gęstości rozkładu obrazują prawdopodobieństwo wylosowania danej wartości, lecz słowo-klucz to "obrazują" - powiedzieliśmy przecież, że dla dowolnego \(x\) mamy \(\mathbb{P}(X=x)=0\). W przypadku gęstości rozkładu nie patrzymy na same wartości funkcji w jakichś punktach, lecz na pola obszarów pod wykresem tej funkcji. Przykładowo, na Ryc. 2. prawdopodobieństwo, że zmienna losowa przyjmie wartość mniejszą lub równą \(x_2\) (na lewo od czarnej pionowej kreski) jest równe polu obszaru zamalowanego kolorem żółtym. Ogólniej mówiąc, \(\mathbb{P}(a\leq X\leq b)\) to pole obszaru ograniczonego:
- od dołu osią \(OX\),
- od góry wykresem funkcji gęstości rozkładu prawdopodobieństwa,
- od prawej prostą \(x=b\),
- od lewej prostą \(x=a\).
Niezbędnym wymogiem, aby funkcja mogła być gęstością jakiegoś rozkładu, jest aby pole pod całym jej wykresem było równe \(1\) - jest to pełna analogia względem sumy wszystkich prawdopodobieństw w przypadkach omawianych wcześniej. Bardziej zaawansowany czytelnik natychmiast powinien zorientować się, co tu jest grane - dla rozkładów ciągłych prawdopodobieństwa wpadnięcia z wartością zmiennej do przedziału \([a, b]\) oblicza się całkując gęstość od \(a\) do \(b\): $$\mathbb{P}(a\leq X\leq b) = \int_{a}^{b}{g(x)dx}$$
Widzimy już, że rozkładów prawdopodobieństwa jest bardzo wiele, a niektóre z nich są w dodatku źródłem potwornych wręcz trudności. Jak można odnaleźć się w takim morzu losowości? Jak orientować się w nieskończonym oceanie wszystkich możliwych rozkładów prawdopodobieństwa? Okazuje się, że istnieje pewien piękny sposób, który umożliwia skuteczną nawigację na spokojnych wodach pomiędzy sztormami. We wspomnianym przed momentem nieskończonym oceanie rozkładów można wyróżnić jedną bardzo szczególną ich rodzinę. Rozkłady do niej należące nazywami rozkładami normalnymi.
Rozkładem normalnym nazwiemy każdy rozkład ciągły, którego gęstość wyraża się wzorem: $$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$ dla pewnych wartości \(\mu\in\mathbb{R},\ \sigma^2 > 0\). Parametr \(\mu\) nazywamy średnią, zaś parametr \(\sigma^2\) - wariancją. Gęstość przedstawiona na Ryc. 2. to właśnie gęstość rozkładu normalnego ze średnią równą \(0\) i wariancją \(1\).
Średnią możemy odczytać wprost z rysunku: jest to \(x\)-owa współrzędna "garbu" wykresu. Wartości wariancji nie da się odczytać wprost z wykresu.
Centralne Twierdzenie Graniczne i jego związek z rozkładem normalnym
Weźmy teraz \(n\) zmiennych losowych i oznaczmy je przez \(X_1, ..., X_n\). Narzućmy warunek, że wszystkie one mają ten sam rozkład i są między sobą niezależne. Rozkład ten może być całkowicie dowolny, może być dyskretny, może też być ciągły. Ważne jest, aby dla każdego iksa był ten sam. Za przykład niech posłuży nam ponownie rzut kostką: wykonaliśmy na przykład \(n=100\) niezależnych od siebie pojedynczych rzutów kostką i zapisaliśmy wyniki \(X_1, ..., X_{100}\) każdego z nich pod pewną zmienną losową. Ponieważ rozkład jest ten sam, średnia dla każdej zmiennej losowej jest taka sama - oznaczmy ją przez \(\mu\) - dla rzutu kostką \(\mu=\frac{1}{6}\) o ile kostka jest symetryczna. Tak samo sprawa ma się z odchyleniem standardowym - każdy iks ma takie samo - oznaczmy je przez \(\sigma\).
Czytelnika zaniepokojonego pierwszą stycznością z pojęciem odchylenia standardowego pragnę uspokoić - proszę mieć w głowie następujący przykład: mając dwie próbki losowe \(\{99, 100, 101\}\) oraz \(\{1, 100, 199\}\) możemy zauważyć, że średnia jest taka sama dla obu prób. Dla pełnego obrazu sytuacji warto podać pewną miarę rozrzutu danych wokół średniej - do tego służy odchylenie standardowe, najczęściej oznaczane grecką sigmą \((\sigma)\). Częściej jednak do mierzenia rozrzutu wokół średniej używa się wariancji, czyli kwadratu odchylenia standardowego. Wariancję prawie zawsze oznacza się przez \(\sigma^2\).
Każdy rozkład prawdopodobieństwa ma swoją średnią oraz swoją wariancję. Wartości te (dla rozkładów ciągłych) oblicza się zwykle na podstawie funkcji gęstości rozkładu, gdyż w ogólnym przypadku nie dają się odczytać na pierwszy rzut oka. Jednak w przypadku rozkładu normalnego średnia i wariancja są od razu jego parametrami, czyli czymś takim jak \(\lambda\) dla rozkładu Poissona. Gdybyśmy chcieli na podstawie podanego powyżej wzoru na gęstość rozkładu normalnego obliczyć średnią i wariancję, dostalibyśmy odpowiednio \(\mu\) oraz \(\sigma^2\).
W tym momencie czytelnik ma pełne prawo być skonfundowany. Tyle hałasu o ten rozkład normalny, tymczasem gęstość ma bardzo skomplikowany wzór, a na dodatek dostajemy dziwną zbieżność parametrów rozkładu z podstawowymi cechami rozkładu, które zwykle należy obliczyć na podstawie funkcji gęstości! Rzeczywiście, przyznajemy że nietrudno się w tym wszystkim zagubić. Aby ostatecznie ukazać potęgę rozkładu normalnego wróćmy do naszych zmiennych losowych \(X_1, ..., X_n\) i spójrzmy na następujące wyrażenie: $$\frac{X_1 +\ ... + X_n}{n}$$
Ryc. 3. Wyrażenie znajdujące się w centrum zainteresowania - średnia arytmetyczna wyników losowań.
Jest ono zmienną losową, zatem ma jakiś rozkład. Centralne Twierdzenie Graniczne w swojej podstawowej wersji orzeka, że gdy \(n\) dąży do nieskończoności, rozkład tego wyrażenia dąży do rozkładu normalnego ze średnią \(\mu\) i wariancją \(\sigma^2\) - tymi samymi, które pochodziły z rozkładu iksów. Dzieje się tak niezależnie od tego, jaki był wyjściowy rozkład pojedynczego iksa!
W praktyce oznacza to, że gdy \(n\) jest duże, możemy traktować wartości wyrażenia z Ryc. 3. jako pochodzące z rozkładu normalnego. Rozkłady normalne są świetnie zbadane oraz ztabelaryzowane, zatem Centralne Twierdzenie Graniczne przenosi ciężar z badania często dziwacznych, nieznanych rozkładów, na analizę dobrze znanego rozkładu normalnego. Jedyną ceną, jaką ponosimy, jest agregacja naszych dziwnych iksów w postać średniej arytmetycznej.
Źródła:
- Ryc. 2. User:HiTe, Public domain, via Wikimedia Commons