Szkoła podstawowa jest miejscem, w którym każdy z nas po raz pierwszy zetknął się z pojęciem kartezjańskiego układu współrzędnych. Pomysł jest bardzo prosty - rysujemy dwie wzajemnie prostopadłe proste, czyli osie układu, oraz zaznaczamy skalę na każdej z nich. Punkt przecięcia osi jest pewnym wyróżnionym, czyli bardzo szczególnym spośród wszystkich, punktem całej płaszczyzny. W takim układzie współrzędnych punkty reprezentowane są przez uporządkowane pary liczb, które nazywamy współrzędnymi kartezjańskimi i z przyzwyczajenia oznaczamy iks oraz igrek.
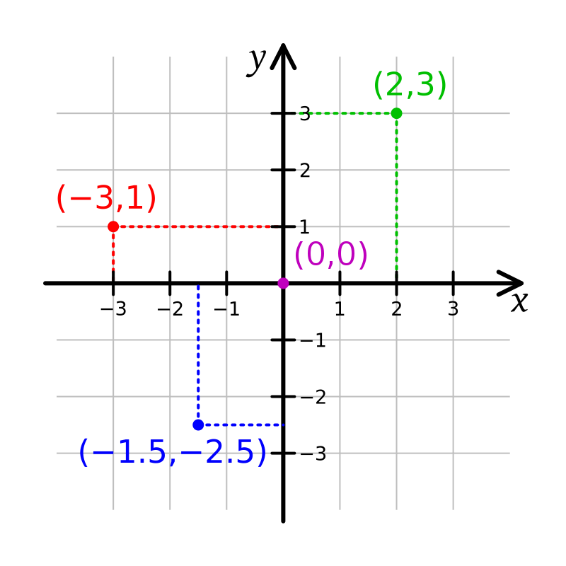
Ryc. 1. Dwuwymiarowy kartezjański układ współrzędnych.
Istnieją też jednak inne układy współrzędnych! I nie chodzi mi nawet o kartezjańską reprezentację przestrzeni trójwymiarowej zamiast dwuwymiarowej płaszczyzny. Nawet na płaszczyźnie istnieją inne układy współrzędnych! Omówię tu jeden: układ współrzędnych biegunowych. Pomysł jest chyba jeszcze prostszy niż w układzie kartezjańskim. Najpierw na całej płaszczyźnie wyróżniamy jedną prostą, oznaczmy ją \(O\). Na prostej \(O\) wyróżniamy pewien punkt, \(S\). Chcąc wyznaczyć współrzędne biegunowe punktu \(P\), spoglądamy na odcinek \(SP\) - ten odcinek ma pewną długość (oczywiście) oraz tworzy z naszą wyróżnioną prostą pewien kąt. To właśnie te dwie liczby – długość i kąt – będą nowymi współrzędnymi naszego punktu: współrzędnymi biegunowymi. Zwyczajowo przyjmujemy oznaczenie \(P=(r,\varphi)\), przy czym oznaczenie długości odcinka \(SP\) literą \(r\) pochodzi od angielskiego radius (pol. promień wodzący).
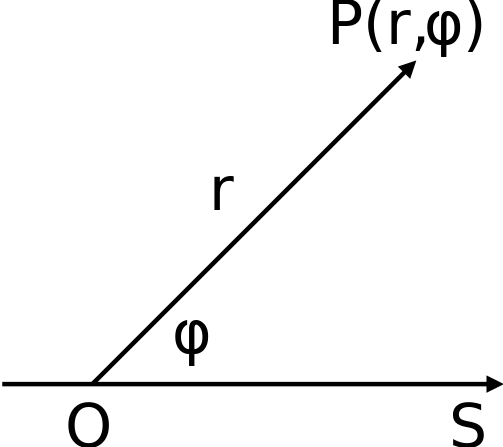
Ryc. 2a. (po lewej) Układ współrzędnych biegunowych w sytuacji ogólnej.
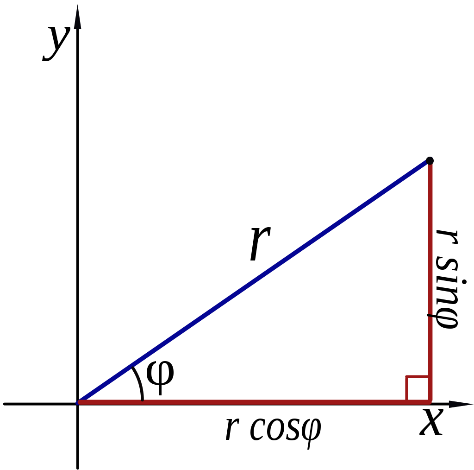
Ryc. 2b. (po prawej) Klasyczny, najczęściej spotykany układ biegunowy.
Ryc. 2b. przedstawia najczęściej spotykaną sytuację, w której wyróżnioną prostą jest oś \(OX\), zaś wyróżnionym punktem - początek układu kartezjańskiego. Związki pomiędzy współrzędnymi kartezjańskimi a biegunowymi opisują dwa równania, wynikające wprost z definicji funkcji trygonometrycznych sinus i cosinus: $$x=r\cdot\cos{\varphi},\qquad y=r\cdot\sin{\varphi}$$ Przykładowo biegunowe współrzędne kartezjańskiego punktu \((1,1)\) to \((\sqrt{2},45^\circ)\). Dociekliwy czytelnik mógłby w tym miejscu okazując poddenerwowanie, spytać o sens i cel takiej zmiany współrzędnych. Po co przechodzić na współrzędne biegunowe? Odpowiedź jest prosta – czasami tak bywa użyteczniej. Weźmy dla przykładu równanie okręgu. W kartezjańskich współrzędnych okrąg o promieniu \(1\) i środku w punkcie \((0,0)\) to krzywa opisana równaniem: $$x^2+y^2=1$$ We współrzędnych biegunowych równanie takiego okręgu to: $$r=1$$ Współrzędnych biegunowych możemy także użyć do opisu… na przykład kwiatków bądź spirali:
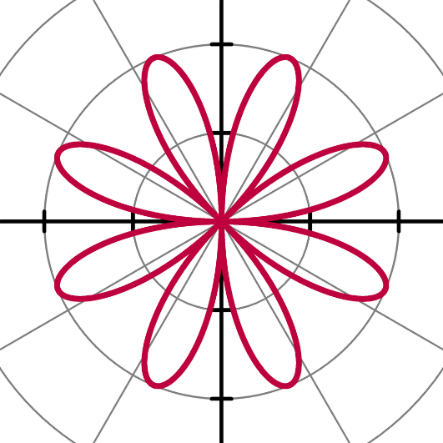
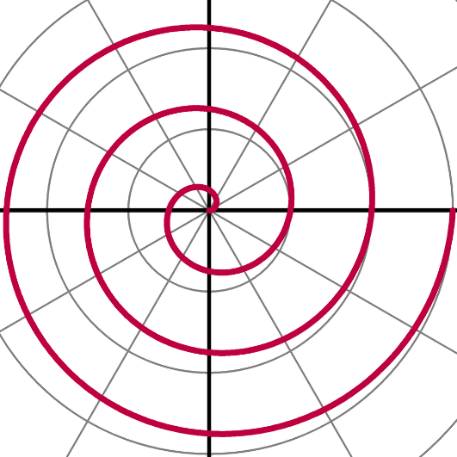
Ryc. 3. Krzywe, których wzory w postaci analitycznej o wiele łatwiej dają się zapisać we współrzędnych biegunowych niż kartezjańskich.
Zadziwiać może prostota równań, które opisują te krzywe. Równanie kwiatka na lewym rysunku to: $$r=2\sin{(4\varphi)}$$ Zaś równanie spirali na prawym rysunku to: $$r=\varphi$$ Dodam jedynie, że zapisanie tych równań we współrzędnych kartezjańskich byłoby arcytrudne, jeśli w ogóle wykonalne. Nie pozostaje mi więc nic innego, jak zachęcić wszystkich zainteresowanych do poeksperymentowania i samodzielnego wykonania kilku podobnych obrazków!
Źródła:
- Ryc. 1. Kbolino, Public domain, via Wikimedia Commons
- Ryc. 2a. Masur, Public domain, via Wikimedia Commons
- Ryc. 2b. No machine-readable author provided. Mets501 assumed (based on copyright claims), CC BY-SA 3.0, via Wikimedia Commons
- Ryc. 3a. Original: Mets501 Vector: Pbroks13, CC BY-SA 3.0, via Wikimedia Commons
- Ryc. 3b. derivative work: Pbroks13 (talk)Archimedian_spiral.PNG: User Mets501 on en.wikipedia, CC BY-SA 3.0, via Wikimedia Commons