„Z niczego stworzyłem cały dziwny wszechświat”, czyli jak rodziła się nowa geometria

Każdy z nas kiedyś uczył się w szkole geometrii. Za ojca tej dziedziny matematyki uchodzi Euklides z Aleksandrii (395 p.n.e. – 270 p.n.e.), który zaproponował badanie geometrii w sposób aksjomatyczny. Euklides podał pięć postulatów, z których wywiódł wszystkie twierdzenia zebrane w dziele, zatytułowanym Elementy. Postulaty te w dzisiejszym języku brzmiałyby tak:

  1. Dowolne dwa punkty można połączyć prostą.
  2. Dowolną prostą można przedłużyć bez ograniczeń.
  3. Dla danego odcinka można zaznaczyć okrąg o środku w dowolnym punkcie i promieniu równym długości tego odcinka.
  4. Wszystkie kąty proste są sobie równe.
  5. Dwie proste, które przecinają trzecią w taki sposób, że suma kątów wewnętrznych po jednej stronie jest mniejsza od sumy dwu kątów prostych, przetną się z tej właśnie strony, jeśli się je odpowiednio przedłuży.
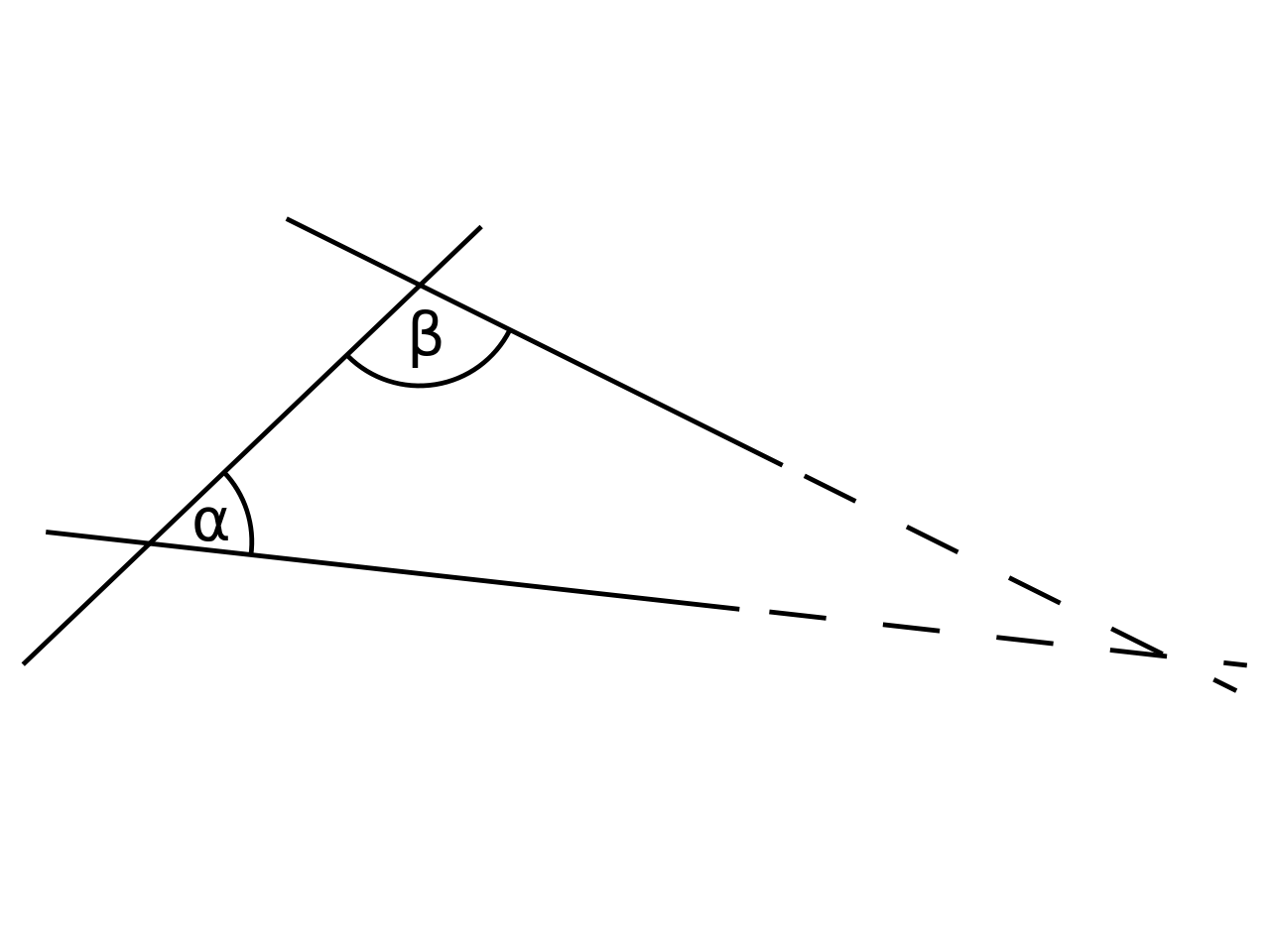
Ilustracja piątego postulatu Euklidesa

Ryc. 1. Wizualizacja piątego postulatu Euklidesa. Suma miar kątów \(\alpha\) i \(\beta\) jest mniejsza od \(180^{\circ}\), zatem przecięcie prostych nastąpi z prawej strony.

Naszą uwagę powinien przykuć postulat piąty, który jest istotnie dłuższy, dziwniejszy i trudniejszy od pozostałych czterech. Późniejsze pokolenia matematyków nie mogły pogodzić się z faktem, że piąty postulat jest aż tak odmienny od pozostałych. Powszechnie wierzono, że lista aksjomatów musi odzwierciedlać piękno geometrii, zaś piąty aksjomat listę tę szpeci.

Stwierdzenie, że piąty postulat wynika z pierwszych czterech (bądź że jego skasowanie prowadzi do sprzeczności), umożliwiłoby skreślenie go z listy. Formalnego dowodu jednak nikt nie potrafił podać, choć wielu próbowało. Przykładowo Giovanni Saccheri (1667-1733) zaprzeczając piątemu postulatowi udowodnił szereg twierdzeń, z których ostatnie mówiło, że istnieje para prostych asymptotycznych. Wówczas stwierdził, że uzyskał sprzeczność z samą naturą linii prostej. Oczywiście nie jest to argument ścisły i wynika raczej z uprzedzeń Saccheriego oraz jego dogmatycznej wiary w geometrię euklidesową. W rzeczywistości jako jeden z pierwszych badał geometrię nieeuklidesową, czego być może w ogóle nie był świadomy.

Co jakiś czas pojawiali się jednak ludzie, którzy badali konsekwencje skasowania piątego postulatu. Pogląd o doskonałości geometrii uprawianej przez Euklidesa powodował jednak, że środowisko matematyków niezwykle nieprzychylnie odnosiło się do takich osób. Skoro ktoś tak genialny jak Euklides umieścił ów piąty postulat na swojej liście, to kimże my jesteśmy, żeby go z tej listy skreślać, czyż nie? Pomimo powszechności takiego myślenia wciąż znajdowali się ludzie, którzy próbowali.

W tym miejscu na scenę wkraczają główni bohaterowie naszej historii. Pierwszym z nich jest Rosjanin Nikołaj Łobaczewski. Jego ojciec, geodeta, zmarł podczas pełnienia obowiązków zawodowych, dzięki czemu młody Nikołaj cały swój proces edukacji mógł odbyć na koszt państwa rosyjskiego. Podczas studiów na uniwersytecie w Kazaniu jego profesorem był Johann Bartels, który wcześniej był nauczycielem Carla Gaussa - jednego z najwybitniejszych matematyków wszech czasów. Gauss już wcześniej interesował się badaniem geometrii bez piątego postulatu, jednakże swoich prac w tym zakresie nie publikował… w obawie przed reakcją środowiska i utratą swojej pozycji. Nie chciał też publicznie powiedzieć, co sądzi na temat „nowej geometrii”. W 1826 roku Łobaczewski zaprezentował swoje dokonania w zakresie badań nad nową geometrią, zaś trzy lata później wydał poświęconą temu tematowi książkę. Wydarzenie to przeszło początkowo bez echa, ponieważ książka wydana została w Kazaniu, w dodatku wyłącznie po rosyjsku. Dopiero w 1840 roku ukazał się przekład dzieła Łobaczewskiego na język niemiecki, który został zauważony przez Gaussa.

Równolegle z Łobaczewskim i całkowicie niezależnie od niego, prace nad geometrią bez piątego postulatu prowadził Węgier Janos Bolyai (czyt. janosz bojoj). Jego ojciec, Farkas (czyt. farkasz), był kolegą Gaussa ze studiów matematycznych. Farkas Bolyai wiele lat swojego życia spędził próbując bezskutecznie wyprowadzić piąty postulat z pierwszych czterech. Uważał, że właśnie przez to nie osiągnął tak wielkiego sukcesu jak jego kolega Gauss. Jego syn również zdecydował się zająć tym tematem, lecz przyjął odmienne podejście. Janos nie próbował udowodnić piątego aksjomatu, lecz zwyczajnie badał konsekwencje jego usunięcia. Po kilku latach studiów i pracy w tym zakresie wysłał do ojca list, w którym o swoich wynikach napisał:

„Odkryłem tak piękne rzeczy, że byłem oczarowany (…) Z niczego stworzyłem cały dziwny wszechświat”

Zainteresowany pracami syna Farkas wysłał je Gaussowi do recenzji. Gauss odpowiedział:

Gdybym rozpoczął od stwierdzenia, że nie jestem w stanie pochwalić tej pracy, przez moment byłbyś zdecydowanie zaskoczony. Nie jestem jednak w stanie stwierdzić inaczej. Gdybym tę pracę pochwalił, pochwaliłbym samego siebie. W rzeczy samej, cała zawartość pracy, ścieżka obrana przez Twojego syna, wyniki do których doszedł, zbiegają się prawie w całości z moimi przemyśleniami, które zajmowały moją głowę częściowo przez ostatnie trzydzieści lub trzydzieści pięć lat.

Okazało się, że Janos w swoich rozważaniach doszedł do tych samych wniosków, co Gauss, całkowicie niezależnie od niego!

Odpowiedź Gaussa skłoniła Bolyai’ów do publikacji wyników Janosa, co stało się w roku 1832. Mimo to Gauss wciąż nie chciał zająć publicznie jasnego stanowiska na temat tego, co sądzi o nowej geometrii. Gdy w roku 1840 Janos Bolyai przeczytał pracę Łobaczewskiego, uznał, że Farkas i Gauss za pośrednictwem Bartelsa sprzedali – bez jego wiedzy - jego prace Rosjanom. Janos Bolyai zmarł w roku 1860, do końca życia wierząc w tę wersję wydarzeń. Podobno przez ostatnie 20 lat swojego życia, czując się okradziony ze swojego dorobku, do nikogo nie powiedział ani słowa. Geometrię, której współtwórcą jest wraz z Łobaczewskim, dziś nazywamy geometrią nieeuklidesową. Powszechnie jest ona uznawana za równoprawną względem geometrii euklidesowej oraz aktywnie rozwijana w badaniach na całym świecie.

Źródła: